Encoding and Querying Graphs in the Relational Model
Encoding and querying graphs in a relational data-store seems to be a challenging task. I discuss the inner workings of act-as-dag gem, a library that is supposed to aid in handling directed and acyclic graphs. I will show that chosen approach has issues1, and moreover that the problem the library tries to solve doesn't exist in the first place. I will also demonstrate how the problem can be solved in a very general manner with just a few lines of code.
This article is largely framework and even programming language agnostic.
Directed, Acyclic Graphs
A directed graph D = (N, A) consist of a set of nodes N and a set of arcs A. An arc is an ordered pair consisting of a source and a target, each referencing a node. In the figure given below, N would be {1, 2, 3} and A would be {(1, 2), (2, 3)}. It is customary do denote the size of N with n and the size of A with m. So, for our example m = 2 holds as well as n = 3.
A Directed, Acyclic Graph
Encoding Digraphs in the Relational Model
A minimal2 schema for a digraph would include a table of nodes with a unique identifier and a table of arcs where each row references a source and target node respectively. Querying the tables (containing our example from above) would yield the following:
SELECT * from nodes; SELECT * from arcs;
id source_id | target_id
--- ----------+-----------
1 1 | 2
2 2 | 3
3Preventing Cycles
A graph is cycle free or acyclic if there exists no path from any node to itself. So, the graph in the picture above is acyclic but the one below is not. Ensuring that a graph stays acyclic upon insertion of an arc (a, b) can be done by asserting that there is no path from b to a.
Introducing a Cycle
An equivalent formulation uses the notion of descendants. The descendants of a node are all those nodes that can be reached by some path originating from the node. The descendants of the node 1 in our figure from above are the nodes 2 and 3, for example. Then, an acyclic graph remains cycle free upon insertion of (a, b) if and only if the descendants of b do not include a. This second formulation is in particular convenient to use when working with the relational model.
The Encoding of the act-as-dag Library
The act-as-dag3 gem is a library for the ruby on rails framework. It appeared in its original version in 2008. It was abandoned quickly by its founder; but has been maintained by others, to be compatible with the framework, up to the time of this writing.
Objective
The objective of the act-as-dag library is to ensure acyclicity, as well as finding all descendants (resp. ancestors) of a node. Now, performing these tasks is rather trivial by adapting graph traversal strategies like breadth or depth first search slightly.
What is left for the act-as-dag is to minimize the number of required queries4. The authors suggest in their documentation that the number of queries is asymptotically equivalent to performing general graph traversal, which is in θ(m). I will contradict this assumption in a few paragraphs down; but let us have a closer look at the act-as-dag internals first.
Encoding
The act-as-dag adds additional, "internal" arcs to the given graph. It links every node with all of its descendants and ancestors. This is illustrated with the dotted arcs in the figure below.
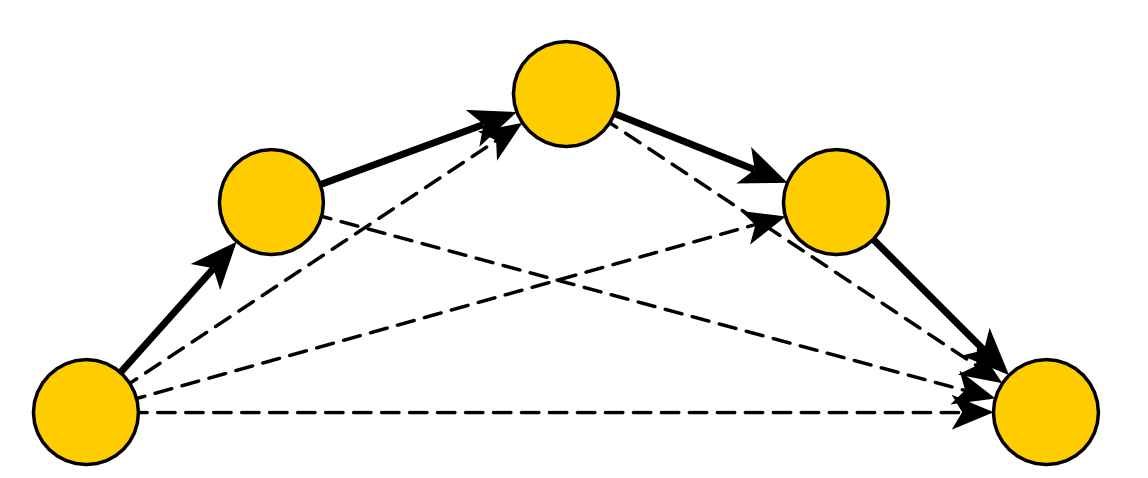
Additional, Internal Arcs
It is now absolutely trivial to query all the descendants or predecessors of a node. Unfortunately, this comes with some costs.
Costs and Size
The drawbacks are conveniently highlighted by a graph of two stars, each of n/2 nodes as shown in this paragraph. When the red, dotted arc is added each blue node must be connected to each green node. Now, the encoding applied by act-as-dag requires to store m ∈ θ(n2) edges where the original graph still has only a few edges, that is m ∈ O(n). The operation of deleting or inserting the red arc requires effort in θ(n2) too.
Connecting two Stars
It must be noted that practically all large real world networks are sparse5. They have much fewer edges than there would be possible, i.e. m«n2. Constructed graphs that are supposed to model real-world networks fulfill m ∈ O(n log n) or even m ∈ O(n). So, for substantial networks an encoding as applied by act-as-dag is problematic. This is in particular true when considering relational datastores where the performance relies highly on caching to avoid random seeks on hard disks6.
A better Approach
It is not true that we need to perform in the order of O(m) queries to retrieve all descendants or ancestors of a node. I will show two possible ways to perform the operation in either just one (slightly more complex) SQL query or with very few basic SQL queries.
Using Common Table Expressions
The first technique relies on a recursive with query, also known as a common table expression. The provided example returns all descendants of the node with the smallest id on a schema as indicated earlier. I will not discuss how such queries work in general, this is well documented by many resources, e.g. on MSDN or ProstgreSQL's with-queries documentation. The queries used in this post as well as a minimal schema and an example network corresponding to Figure Breath First Search are provided with this article. The next section will provide deeper insight with respect to graphs in particular.
-- example: all descendants of the node with id = 1
WITH RECURSIVE pair(s,t) AS (
SELECT source_id as s, target_id as t FROM arcs where source_id = 1
UNION
SELECT source_id, target_id from pair, arcs WHERE source_id = t)
SELECT DISTINCT t from pair ORDER BY t ;
The query as given above will run without modification on PostgreSQL. It will run on other products with only minimal modification if any at all. However, it won't run in particular on MySQL or sqlite3, which simply do not support CTEs. Not all is lost though; even, if you are required to use a product without support for CTEs.
Using Basic Queries
Let us perform a gedankenexperiment. Consider the graph as depicted below. Assume we start with the yellow node. We then follow each outgoing arc and discover all blue nodes. Next, we consider all arcs leaving the blue nodes, and discover all green nodes. This is the principle of breath first search (BFS).
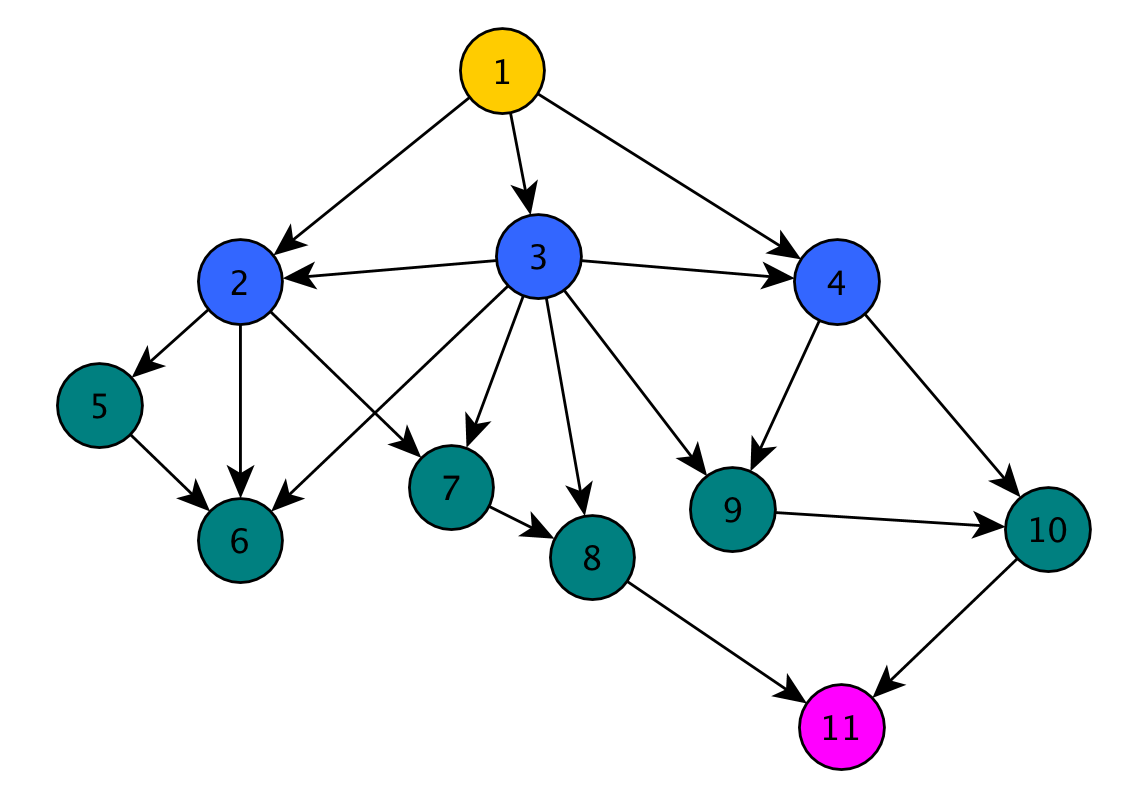
Breadth First Search
SELECT target_id FROM arcs WHERE source_id in ( 1 );
SELECT target_id FROM arcs WHERE source_id in (2,3,4);
The key observation is that we don't have to query each arc in separation7. We can use a minimalistic8 subquery9 instead. The query as displayed above will return all green nodes at once. We can then retrieve all descendants of the yellow node with just two queries.
Nesting Subqueries and CTEs
We can even write a nested subquery to get all descendants of the yellow node with just one query. The following query returns the descendants which are separated from the starting node by no more than two arcs:
SELECT target_id FROM arcs WHERE source_id in (1)
UNION
SELECT target_id FROM arcs WHERE source_id in
( SELECT target_id FROM arcs WHERE source_id in (1))
ORDER BY target_id;
The similarities to CTEs are apparent. Essentially, CTEs allow us to formulate for infinite depth10. The question is now how many levels of nesting (or how many unnested queries) are necessary. This can be answered through the diameter of a graph.
The Diameter of Networks
The number of queries to retrieve all descendants is bound by the diameter of the graph under consideration. The diameter is one of the many distance measures in networks. The precise definition requires a few other concepts that I did not introduce, and don't matter to us.
What is important in our context is that real-world networks tend to have a very small diameter compared to their overall size. This statement is backed by numerous studies. Stanley Milgram, for example, performed a famous experiment which resulted in the concept of six degrees of separation.
An alternative to the act-as-dag gem
Technical Issues of the act-as-dag gem
The encoding, as used by the act-as-dag gem, has little to offer and introduces a number of drawbacks which lead to scalability and performance problems. From a technical stand point, the implementation might have been acceptable in 2008. However, the integration for rails 3 is suboptimal at best. It lacks in particular chainable and composable queries that were introduced with arel.
A Better Alternative
I created a sample ruby on rails project called digraph-demo to demonstrate how the suggested alternative could be implemented. It is based on using subqueries to retrieve all descendants with a few queries as outlined previously.
It has numerous advantages over the act-as-dag approach:
It scales well; no additional entities or even structures are stored other than necessary to store the graph itself.
It performs well over a wide range of operations with no mentionable weak spots.
It is very general. It not only supports acyclic graphs, but also
- general digraphs,
- trees,
- selfloops,
- backloops,
- multiarcs, and even
- undirected graphs11.
It is still considerably simpler (less than 100 lines in
app/models) compared to the act-as-dag gem (more than 800 lines inlib).It integrates seamlessly with rails 3 chainable queries and thus fosters reuse.
Conclusion
There is no reason to put up with the deficiencies of the act-as-dag gem and potentially other libraries that follow the same strategy. The addressed problem can be solved by simple SQL queries without mentionable performance or other drawbacks.
Many of the deficiencies are communicated clearly. This seems not to hinder engineers use it anyways, be it of ignorance or for other reasons.↩
Well, a truly minimal schema would not include an explicit table for the nodes.↩
A fork that represents the state of act-as-dag at the time of writing is available on my github repositories.↩
Just minimizing the number of queries is often a rather near sighted approach to provide performance.↩
Supporting this statement is out of the scope of this article. I invite the interested reader to start with reading my dissertation, for example.↩
At some point, the memory required for the additional edges will surpass the available RAM. The performance of the application as a whole, and in particular not only the graph queries, will start to degenerate.↩
The database system will still have to evaluate each out-arc, but there is only one query involved.↩
It is technically really a subquery since we use the
INcomparison operator.↩I hinted to the benefits of using subqueries in a previous post.↩
It is possible to write recursive with statements that get stuck in an infinite loop; resulting in a stack overflow at some point.↩
Note that it is very simple to extend to an undirected graph on the basis of a digraph by automatically adding links in the opposite direction. However, I wouldn't recommend to proceed in this way since algorithms for undirected/directed graphs often differ in subtle ways.↩
